

CN 11-1911/B


Acta Psychologica Sinica ›› 2023, Vol. 55 ›› Issue (6): 994-1015.doi: 10.3724/SP.J.1041.2023.00994
• Reports of Empirical Studies • Previous Articles Next Articles
HUANG Yuanna1,2, JIANG Chengming3, LIU Hongzhi4, LI Shu2,5,*( )
)
Received:2022-02-13
Published:2023-06-25
Online:2023-03-10
Contact:
LI Shu
E-mail:lishu@psych.ac.cn
Supported by:HUANG Yuanna, JIANG Chengming, LIU Hongzhi, LI Shu. (2023). Toward a coherent understanding of risky, intertemporal, and spatial choices: Evidence from eye-tracking and subjective evaluation. Acta Psychologica Sinica, 55(6), 994-1015.
Add to citation manager EndNote|Ris|BibTeX
URL: https://journal.psych.ac.cn/acps/EN/10.3724/SP.J.1041.2023.00994
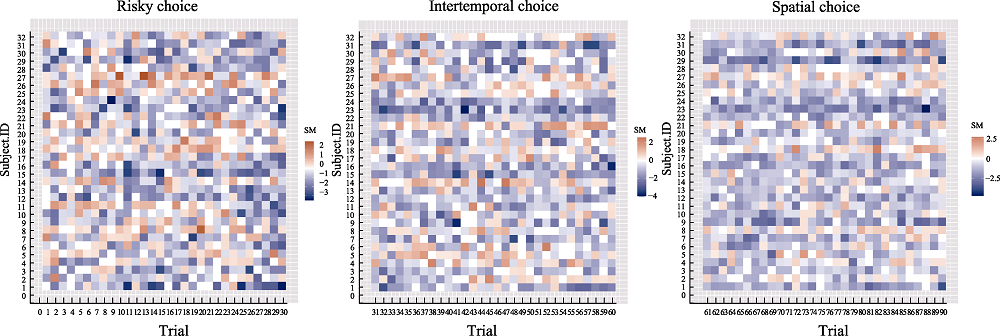
Figure 8. Heat map of SM values at the individual level, where the horizontal axis represents all trials in each domain; the vertical axis represents the number of each participant, blue represents SM values smaller than 0, and red represents SM values greater than 0.
| Risky choice | Intertemporal choice | Spatial choice | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Choice preference | Visual analogue scale | Choice preference | Visual analogue scale | Choice preference | Visual analogue scale | ||||||||
| Computational difficulty | Parameter | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD |
| Low | First pairs | 4.66 (B) | 1.35 | 3.22 | 1.69 | 4.94 (B) | 1.58 | 2.60 | 2.15 | 3.13 (A) | 1.83 | 4.05 | 2.13 |
| Second pairs | 1.67 (C) | 1.2 | 5.23 | 2.32 | 1.57 (C) | 1.18 | 5.32 | 2.26 | 1.34 (C) | 1.02 | 5.67 | 2.08 | |
| High | First pairs | 4.85 (B) | 1.37 | 3.09 | 1.55 | 5.41 (B) | 1.12 | 2.36 | 2.17 | 3.01 (A) | 1.95 | 4.30 | 2.21 |
| Second pairs | 1.96 (C) | 1.51 | 5.25 | 2.06 | 2.12 (C) | 1.66 | 4.88 | 2.28 | 1.50 (C) | 1.28 | 5.52 | 2.27 | |
Table 1 Descriptive statistic results for the three choice domains
| Risky choice | Intertemporal choice | Spatial choice | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Choice preference | Visual analogue scale | Choice preference | Visual analogue scale | Choice preference | Visual analogue scale | ||||||||
| Computational difficulty | Parameter | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD |
| Low | First pairs | 4.66 (B) | 1.35 | 3.22 | 1.69 | 4.94 (B) | 1.58 | 2.60 | 2.15 | 3.13 (A) | 1.83 | 4.05 | 2.13 |
| Second pairs | 1.67 (C) | 1.2 | 5.23 | 2.32 | 1.57 (C) | 1.18 | 5.32 | 2.26 | 1.34 (C) | 1.02 | 5.67 | 2.08 | |
| High | First pairs | 4.85 (B) | 1.37 | 3.09 | 1.55 | 5.41 (B) | 1.12 | 2.36 | 2.17 | 3.01 (A) | 1.95 | 4.30 | 2.21 |
| Second pairs | 1.96 (C) | 1.51 | 5.25 | 2.06 | 2.12 (C) | 1.66 | 4.88 | 2.28 | 1.50 (C) | 1.28 | 5.52 | 2.27 | |
| Computatial difficulty (Low) | Computatial difficulty (High) | ||
|---|---|---|---|
| Risky choice | First pair | A: (¥6, 000, 45%) B:(¥3, 000, 90%) | A: (¥9, 500, 65%) B: (¥6, 500, 95%) |
| Second pair | C: (¥6, 000, 0.1%) D: (¥3, 000, 0.2%) | C: (¥9, 500, 0.65%) D: (¥6, 500, 0.85%) | |
| Third pair | C: (¥6, 000, 36%) D: (¥3, 000, 72%) | C: (¥9, 500, 58%) D: (¥6, 500, 85%) | |
| Intertemporal choie | First pair | A: (¥6, 000, 20 years) B: (¥3, 000, 10 years) | A: (¥9, 500, 30 years) B: (¥6, 500, 10 years) |
| Second pair | C: (¥6, 000, 20 days) D: (¥3, 000, 10 days) | C: (¥9, 500, 30 days) D: (¥6, 500, 10 days) | |
| Third pair | C: (¥6, 000, 16 years) D: (¥3, 000, 8 years) | C: (¥9, 500, 27 years) D: (¥6, 500, 9 years) | |
| Spatial choice | First pair | A: (¥6, 000, 1, 800 km) B: (¥3, 000, 900 km) | A: (¥9, 500, 600 km) B: (¥6, 500, 200 km) |
| Second pair | C: (¥6, 000, 4 km) D: (¥3, 000, 2 km) | C: (¥9, 500, 3 km) D: (¥6, 500, 1 km) | |
| Third pair | C: (¥6, 000, 1, 440 km) D: (¥3, 000, 720 km) | C: (¥9, 500, 540 km) D: (¥6, 500, 180 km) |
| Computatial difficulty (Low) | Computatial difficulty (High) | ||
|---|---|---|---|
| Risky choice | First pair | A: (¥6, 000, 45%) B:(¥3, 000, 90%) | A: (¥9, 500, 65%) B: (¥6, 500, 95%) |
| Second pair | C: (¥6, 000, 0.1%) D: (¥3, 000, 0.2%) | C: (¥9, 500, 0.65%) D: (¥6, 500, 0.85%) | |
| Third pair | C: (¥6, 000, 36%) D: (¥3, 000, 72%) | C: (¥9, 500, 58%) D: (¥6, 500, 85%) | |
| Intertemporal choie | First pair | A: (¥6, 000, 20 years) B: (¥3, 000, 10 years) | A: (¥9, 500, 30 years) B: (¥6, 500, 10 years) |
| Second pair | C: (¥6, 000, 20 days) D: (¥3, 000, 10 days) | C: (¥9, 500, 30 days) D: (¥6, 500, 10 days) | |
| Third pair | C: (¥6, 000, 16 years) D: (¥3, 000, 8 years) | C: (¥9, 500, 27 years) D: (¥6, 500, 9 years) | |
| Spatial choice | First pair | A: (¥6, 000, 1, 800 km) B: (¥3, 000, 900 km) | A: (¥9, 500, 600 km) B: (¥6, 500, 200 km) |
| Second pair | C: (¥6, 000, 4 km) D: (¥3, 000, 2 km) | C: (¥9, 500, 3 km) D: (¥6, 500, 1 km) | |
| Third pair | C: (¥6, 000, 1, 440 km) D: (¥3, 000, 720 km) | C: (¥9, 500, 540 km) D: (¥6, 500, 180 km) |
| [1] |
Ares, G., Mawad, F., Giménez, A., & Maiche, A. (2014). Influence of rational and intuitive thinking styles on food choice: Preliminary evidence from an eye-tracking study with yogurt labels. Food Quality and Preference, 31, 28-37. https://doi.org/10.1016/j.foodqual.2013.07.005
doi: https://doi.org/10.1016/j.foodqual.2013.07.005 URL |
| [2] |
Basu, S., & Savani, K. (2017). Choosing one at a time? Presenting options simultaneously helps people make more optimal decisions than presenting options sequentially. Organizational Behavior and Human Decision Processes, 139, 76-91.
doi: 10.1016/j.obhdp.2017.01.004 URL |
| [3] | Ben-Akiva, M., & Lerman, S. R. (1985). Discrete choice analysis: Theory and applications to travel demand. Cambridge, MA: MIT Press. |
| [4] |
Birnbaum, M.H. (2018). Behavioral models of decision making under risk. In: Raue M., Lermer E., Streicher B. (eds) Psychological Perspectives on Risk and Risk Analysis. Springer, Cham. https://doi.org/10.1007/978-3-319-92478-6_8
doi: https://doi.org/10.1007/978-3-319-92478-6_8 |
| [5] |
Böckenholt, U., & Hynan, L. S. (1994). Caveats on a process-tracing measure and a remedy. Journal of Behavioral Decision Making, 7(2), 103-117. https://doi.org/10.1002/bdm.3960070203
doi: https://doi.org/10.1002/bdm.3960070203 URL |
| [6] |
Boroditsky, L. (2000). Metaphoric structuring: Understanding time through spatial metaphors. Cognition, 75(1), 1-28.
pmid: 10815775 |
| [7] |
Brandstätter, E., & Gussmack, M. (2013). The cognitive processes underlying risky choice. Journal of Behavioral Decision Making, 26(2), 185-197. https://doi.org/10.1002/bdm.1752
doi: https://doi.org/10.1002/bdm.1752 URL |
| [8] |
Brandstätter, E., & Körner, C. (2014). Attention in risky choice. Acta Psychologica, 152, 166-176. https://doi.org/10.1016/j.actpsy.2014.08.008
doi: 10.1016/j.actpsy.2014.08.008 pmid: 25226548 |
| [9] |
Brandstätter, E., Gigerenzer, G., & Hertwig, R. (2006). The priority heuristic: Making choices without trade-offs. Psychological Review, 113(2), 409-432. https://doi.org/10.1037/0033-295X.113.2.409
doi: 10.1037/0033-295X.113.2.409.113.2.409 pmid: 16637767 |
| [10] | Bueti, D., & Walsh, V. (2009). The parietal cortex and the representation of time, space, number and other magnitudes. Philosophical Transactions of the Royal Society of London, 364(1525), 1831-1840. |
| [11] |
Buzsáki, G., & Llinás, R. (2017). Space and time in the brain. Science, 358(6362), 482-485.
doi: 10.1126/science.aan8869 pmid: 29074768 |
| [12] |
Carstensen, L. L. (2006). The influence of a sense of time on human development. Science, 312(5782), 1913-1915. https://doi.org/10.1126/science.1127488
doi: 10.1126/science.1127488 pmid: 16809530 |
| [13] |
Cheng, J., & González-Vallejo, C. (2016). Attribute-wise vs. alternative-wise mechanism in intertemporal choice: Testing the proportional difference, trade-off, and hyperbolic models. Decision, 3(3), 190-215. https://doi.org/10.1037/dec0000046
doi: https://doi.org/10.1037/dec0000046 URL |
| [14] |
Chen, H. X., & He, G. B. (2011). The effect of construal level on intertemporal choice and risky choice. Acta Psychologica Sinica, 43(4), 442-452.
doi: 10.3724/SP.J.1041.2011.00442 URL |
| [15] |
Dai, J., & Busemeyer, J. R. (2014). A probabilistic, dynamic, and attribute-wise model of intertemporal choice. Journal of Experimental Psychology: General, 143(4), 1489-1514. https://doi.org/10.1037/a0035976
doi: https://doi.org/10.1037/a0035976 URL |
| [16] |
Ding, X., Feng, N., Cheng, X., Liu, H., & Fan, Z. (2015). Are past and future symmetric in mental time line? Frontiers in Psychology, 6, 208-215
doi: 10.3389/fpsyg.2015.00208 pmid: 25767457 |
| [17] |
Eikmeier, V., Schröter, H., Maienborn, C., Alex-Ruf, S., & Ulrich, R. (2013). Dimensional overlap between time and space. Psychonomic Bulletin & Review, 20(6), 1120-1125.
doi: 10.3758/s13423-013-0431-2 URL |
| [18] |
Faul, F., Erdfelder, E., Buchner, A., & Lang, A. G. (2009). Statistical power analyses using G* Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41(4), 1149-1160. https://doi.org/10.3758/BRM.41.4.1149
doi: https://doi.org/10.3758/BRM.41.4.1149 URL |
| [19] | Fisher, I. (1930). The theory of interest as determined by impatience to spend income and opportunity to invest it. New York: Macmillan. |
| [20] |
Frederick, S., Loewenstein, G., & O'Donoghue, T. (2002). Time discounting and time preference: A critical review. Journal of Economic Literature, 40(2), 351-401. http://dx.doi.org/10.3758/s13423-015-0879-3
doi: http://dx.doi.org/10.3758/s13423-015-0879-3 URL |
| [21] |
Gigerenzer, G., and Goldstein, D.G. (1996). Reasoning the fast and frugal way: Models of bounded rationality. Psychological Review. 103, 650-669. http://dx.doi.org/10.1037/0033-295x.103.4.650
doi: http://dx.doi.org/10.1037/0033-295x.103.4.650 pmid: 8888650 |
| [22] |
Glaholt, M. G., & Reingold, E. M. (2011). Eye movement monitoring as a process tracing methodology in decision making research. Journal of Neuroscience, Psychology, and Economics, 4(2), 125-146. https://doi.org/10.1037/a0020692
doi: https://doi.org/10.1037/a0020692 URL |
| [23] |
Glöckner, A., & Herbold, A. K. (2011). An eye-tracking study on information processing in risky decisions: Evidence for compensatory strategies based on automatic processes. Journal of Behavioral Decision Making, 24(1), 71-98. http://dx.doi.org/10.1002/bdm.684
doi: http://dx.doi.org/10.1002/bdm.684 URL |
| [24] |
Green, L., Fristoe, N., & Myerson, J. (1994). Temporal discounting and preference reversals in choice between delayed outcomes. Psychonomic Bulletin & Review, 1(3), 383-389. http://dx.doi.org/10.3758/BF03213979
doi: http://dx.doi.org/10.3758/BF03213979 URL |
| [25] |
Green, L., & Myerson, J. (2004). A discounting framework for choice with delayed and probabilistic rewards. Psychological Bulletin, 130(5), 769-792. https://doi.org/10.1037/0033-2909.130.5.769
doi: 10.1037/0033-2909.130.5.769 pmid: 15367080 |
| [26] |
Hayes, A. F. (2009). Beyond Baron and Kenny: Statistical mediation analysis in the new millennium. Communication Monographs, 76(4), 408-420. https://doi.org/10.1080/03637750903310360
doi: https://doi.org/10.1080/03637750903310360 URL |
| [27] |
He, T. Y., Ding, Y., Li, H. K., Cheng, X. R., Fam, Z., & Ding, X. F. (2020). The multidimensional spatial representation of time: Dissociations on its ontogenetic origin and activation mechanism. Advances in Psychological Science, 28(6), 935-944.
doi: 10.3724/SP.J.1042.2020.00935 URL |
| [28] |
Hertwig, R., & Ortmann, A. (2001). Experimental practices in economics: A methodological challenge for psychologists? Behavioral and Brain Sciences, 24(3), 383-403.
pmid: 11682798 |
| [29] | Horn, S., & Freund, A. M. (2022). Adult age differences in monetary decisions with real and hypothetical reward. Journal of Behavioral Decision Making, 35(2), e2253. |
| [30] |
Jiang, C. M., Liu, H. Z., Cai, X. H., & Li, S. (2016). A process test of priority models of intertemporal choice. Acta Psychologica Sinica, 48(1), 59-72. http://dx.doi.org/10.3724/SP.J.1041.2016.00059
doi: http://dx.doi.org/10.3724/SP.J.1041.2016.00059 URL |
| [31] |
Jiang, D., & He, G. B. (2017). Decision making: Based on the perspective of psychological distance. Advances in Psychological Science, 25(11), 1992-2001.
doi: 10.3724/SP.J.1042.2017.01992 URL |
| [32] | Jeffreys, H. (1961). Theory of probability (3rd ed.). Oxford, UK: Oxford University Press. |
| [33] |
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263-291. https://doi.org/10.2307/1914185
doi: https://doi.org/10.2307/1914185 URL |
| [34] | Keeney, R. L., & Raiffa, H. (1976). Decisions with multiple objectives: Preferences and value trade-offs. Wiley, New York. |
| [35] |
Kuang, Y., Huang, Y. N., & Li, S. (2022). A framing effect of intertemporal and spatial choice. Quarterly Journal of Experimental Psychology, https://doi.org/10.1177/17470218221113519.
doi: https://doi.org/10.1177/17470218221113519 |
| [36] |
Kundel, H. L., Nodine, C. F., Conant, E. F., & Weinstein, S. P. (2007). Holistic component of image perception in mammogram interpretation: Gaze-tracking study. Radiology, 242(2), 396-402.
doi: 10.1148/radiol.2422051997 pmid: 17255410 |
| [37] |
Lakoff, G., & Johnson, M. (1980). The metaphorical structure of the human conceptual system. Cognitive Science, 4(2), 195-208.
doi: 10.1207/s15516709cog0402_4 URL |
| [38] | Lee., L & Anderson, R. (2009). A comparison of compensatory and noncompensatory decision making strategies in IT project portfolio management. In International Research Workshop on IT Project Management 2009 (p.9). http://aisel.aisnet.org/irwitpm2009/9 |
| [39] | Li, S. (2016). An equate-to-differentiate way of decision-making. Shanghai: East China Normal University Press. |
| [40] | Li, S. (2005). Choice reversals across certainty, uncertainty and risk: The equate-to-differentiate interpretation. Acta Psychologica Sinica, 37(4), 427-433. |
| [41] |
Li, S. (2004). A behavioral choice model when computational ability matters. Applied Intelligence, 20(2), 147-163. http://dx.doi.org/10.1023/B:APIN.0000013337.01711.c7
doi: http://dx.doi.org/10.1023/B:APIN.0000013337.01711.c7 URL |
| [42] |
Li, S. (1998). Can the conditions governing the framing effect be determined? Journal of Economic Psychology, 19(1), 133-153. https://doi.org/10.1016/S0167-4870(97)00039-1
doi: https://doi.org/10.1016/S0167-4870(97)00039-1 URL |
| [43] | Li, S. (1994). Equate-to-differentiate theory: A coherent bi-choice model across certainty, uncertainty and risk. University of New South Wales. |
| [44] |
Liu, H. Z., Jiang, C. M., Rao, L. L., & Li, S. (2015). Discounting or priority: Which rule dominates the intertemporal choice process? Acta Psychologica Sinica, 47(4), 522-532. https://doi.org/10.3724/SP.J.1041.2015.00522
doi: https://doi.org/10.3724/SP.J.1041.2015.00522 URL |
| [45] |
Loewenstein, G., & Prelec, D. (1992). Anomalies in intertemporal choice: Evidence and an interpretation. Quarterly Journal of Economics, 107(2), 573-597. https://doi.org/10.2307/2118482
doi: https://doi.org/10.2307/2118482 URL |
| [46] | May, J., & Thrift, N. (Eds.). (2001). Timespace: Geographies of temporality. London: Routledge |
| [47] | Mazur, J. E. (1987). An adjusting procedure for studying delayed reinforcement. In M. L. Commons, J. E. Mazur, J. A. Nevin, & H. Rachlin (Eds.), Quantitative analysis of behavior: The effect of delay and of intervening events on reinforcement value (pp. 55-73). Hillsdale, NJ: Erlbaum. |
| [48] |
McGraw, A. P., Larsen, J. T., Kahneman, D., & Schkade, D. (2010). Comparing gains and losses. Psychological Science, 21(10), 1438-1445. https://doi.org/10.1177/0956797610381504
doi: 10.1177/0956797610381504 pmid: 20739673 |
| [49] | Norman, E., & Schulte-Mecklenbeck, M. (2010). Take a quick click at that! Mouselab and eye-tracking as tools to measure intuition. Foundations for Ttracing Intuition: Challenges and Methods, 24-44. |
| [50] |
Olschewski, S., & Rieskamp, J. (2020). Distinguishing three effects of time pressure on risk taking: Choice consistency, risk preference, and strategy selection. Journal of Behavioral Decision Making,1-14. http://dx.doi.org/10.1002/bdm.2228
doi: http://dx.doi.org/10.1002/bdm.2228 |
| [51] |
Pachur, T., Hertwig, R., Gigerenzer, G., & Brandstätter, E. (2013). Testing process predictions of models of risky choice: A quantitative model comparison approach. Frontiers in Psychology, 4, 646. https://doi.org/10.3389/fpsyg.2013.00646
doi: 10.3389/fpsyg.2013.00646 pmid: 24151472 |
| [52] |
Payne, J. W. (1994). Thinking aloud: Insights into information processing. Psychological Science. 5(5), 241-248. https://doi.org/10.1111/j.1467-9280.1994.tb00620.x
doi: https://doi.org/10.1111/j.1467-9280.1994.tb00620.x |
| [53] |
Payne, J. W., & Braunstein, M. L. (1978). Risky choice: An examination of information acquisition behavior. Memory & Cognition, 6(5), 554-561. http://dx.doi.org/10.3758/BF03198244
doi: http://dx.doi.org/10.3758/BF03198244 URL |
| [54] | Payne, J.W., Bettman, J.R., & Johnson, E.J. (1993). The Adaptive Decision Maker. Cambridge University Press: New York |
| [55] |
Payne, J. W., Bettman, J. R., & Johnson, E. J. (1988). Adaptive strategy selection in decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14, 534-552. https://doi.org/10.1037/0278-7393.14.3.534
doi: https://doi.org/10.1037/0278-7393.14.3.534 URL |
| [56] |
Pellegrini, P. A., & Fotheringham, A. S. (2002). Modelling spatial choice: A review and synthesis in a migration context. Progress in Human Geography, 26(4), 487-510. https://doi.org/10.1191/0309132502ph382ra
doi: https://doi.org/10.1191/0309132502ph382ra URL |
| [57] |
Podsakoff, P. M., MacKenzie, S. B., Lee, J.-Y., & Podsakoff, N. P. (2003). Common method biases in behavioral research: A critical review of the literature and recommended remedies. Journal of Applied Psychology, 88(5), 879-903.
doi: 10.1037/0021-9010.88.5.879 pmid: 14516251 |
| [58] |
Prelec, D., & Loewenstein, G. (1991). Decision making over time and under uncertainty: A common approach. Management Science, 37(7), 770-786. https://doi.org/10.1287/mnsc.37.7.770
doi: https://doi.org/10.1287/mnsc.37.7.770 URL |
| [59] |
Rachlin, H. (2006). Notes on discounting. Journal of the Experimental Analysis of Behavior, 85, 425-435. http://dx.doi.org/10.1901/jeab.2006.85-05
doi: http://dx.doi.org/10.1901/jeab.2006.85-05 pmid: 16776060 |
| [60] |
Rachlin, H., Brown, J., & Cross, D. (2000). Discounting in judgments of delay and probability. Journal of Behavioral Decision Making, 13(2), 145-159.
doi: 10.1002/(ISSN)1099-0771 URL |
| [61] |
Rao, L. L., Li, S., Jiang, T., & Zhou, Y. (2012). Is payoff necessarily weighted by probability when making a risky choice? Evidence from functional connectivity analysis. PLoS One, 7(7), e41048. http://dx.doi.org/10.1371/journal.pone.0041048
doi: http://dx.doi.org/10.1371/journal.pone.0041048 URL |
| [62] |
Rao, L. L., Liu, X. N., Li, Q., Zhou, Y., Liang, Z. Y., Sun, H. Y., … Li, S. (2013). Toward a mental arithmetic process in risky choices. Brain and Cognition, 83(3), 307-314. http://dx.doi.org/10.1016/j.bandc.2013.09.009
doi: 10.1016/j.bandc.2013.09.009 pmid: 24128658 |
| [63] |
Ratcliff, R., Smith, P. L., Brown, S. D., & McKoon, G. (2016). Diffusion decision model: Current issues and history. Trends in Cognitive Sciences, 20(4), 260-281.
doi: S1364-6613(16)00025-5 pmid: 26952739 |
| [64] | Read, D. (2004). Intertemporal choice. Blackwell handbook of judgment and decision making, 424-443. |
| [65] |
Reeck, C., Wall, D., & Johnson, E. J. (2017). Search predicts and changes patience in intertemporal choice. Proceedings of the National Academy of Sciences, 114(45), 11890-11895. https://doi.org/10.1073/pnas.1707040114
doi: https://doi.org/10.1073/pnas.1707040114 URL |
| [66] | Rotter, J. B. (1954). Social learning and clinical psychology. New York: Prentice-Hall. |
| [67] | Sarukkai, S. (2009). Phenomenology of untouchability. Economic and Political Weekly, 44(37), 39-48. |
| [68] |
Savage, L. J. (1951) The theory of statistical decision. Journal of the American Statistical Association, 46(253), 55-67. https://doi.org/10.1080/01621459.1951.10500768
doi: https://doi.org/10.1080/01621459.1951.10500768 URL |
| [69] | Savage, L. J. (1954). The foundations of statistics (2nd ed.). New York: Dover. |
| [70] |
Schoemann, A. M., Boulton, A. J., & Short, S. D. (2017). Determining power and sample size for simple and complex mediation models. Social Psychological and Personality Science, 8(4), 379-386. http://dx.doi.org/10.1177/1948550617715068
doi: http://dx.doi.org/10.1177/1948550617715068 URL |
| [71] |
Schulte-Mecklenbeck, M., Johnson, J. G., Böckenholt, U., et al. (2017). Process-tracing methods in decision making: On growing up in the 70s. Current Directions in Psychological Science, 26(5), 442-450. http://dx.doi.org/10.1177/0963721417708229
doi: http://dx.doi.org/10.1177/0963721417708229 URL |
| [72] |
Schulte-Mecklenbeck, M., Kühberger, A., & Ranyard, R. (2011). The role of process data in the development and testing of process models of judgment and decision making. Judgment and Decision making, 6(8), 733-739.
doi: 10.1017/S1930297500004162 URL |
| [73] |
Scholten, M., & Read, D. (2014). Prospect theory and the “forgotten” fourfold pattern of risk preferences. Journal of Risk and Uncertainty, 48(1), 67-83. http://dx.doi.org/10.1007/s11166-014-9183-2
doi: http://dx.doi.org/10.1007/s11166-014-9183-2 URL |
| [74] |
Scholten, M., Read, D., & Sanborn, A. (2014). Weighing outcomes by time or against time? Evaluation rules in intertemporal choice. Cognitive Science, 38(3), 399-438. http://dx.doi.org/10.1111/cogs.12104
doi: 10.1111/cogs.12104 pmid: 24404941 |
| [75] |
Scholten, M., & Read, D. (2010). The psychology of intertemporal tradeoffs. Psychological Review, 117, 925-944. https://doi.org/10.1037/a0019619
doi: 10.1037/a0019619 pmid: 20658858 |
| [76] |
Smythe, E. J., & Goldstone, S. (1957). The time sense: A normative, genetic study of the development of time perception. Perceptual and Motor Skills, 7(1), 49-59. http://dx.doi.org/10.2466/PMS.7.49-59
doi: http://dx.doi.org/10.2466/PMS.7.49-59 URL |
| [77] |
Sheppard, E. S. (1980). The ideology of spatial choice. Papers of the Regional Science Association, 45(1), 197-213. http://dx.doi.org/10.1007/bf01934662
doi: http://dx.doi.org/10.1007/bf01934662 URL |
| [78] |
Su, Y., Rao, L. L., Sun, H. Y., Du, X. L., Li, X., & Li, S. (2013). Is making a risky choice based on a weighting and adding process? An eye-tracking investigation. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39( 6), 1765-1780. http://dx.doi.org/10.1037/a0032861
doi: http://dx.doi.org/10.1037/a0032861 URL |
| [79] |
Stevens, J. R. (2016). Intertemporal similarity: Discounting as a last resort. Journal of Behavioral Decision Making, 29(1), 12-24. http://dx.doi.org/10.1002/bdm.1870
doi: http://dx.doi.org/10.1002/bdm.1870 URL |
| [80] |
Takagaki, K., & Krug, K. (2020). The effects of reward and social context on visual processing for perceptual decision-making. Current Opinion in Physiology, 16, 109-117.
doi: 10.1016/j.cophys.2020.08.006 URL |
| [81] |
Tversky, A. (1969). Intransitivity of preferences. Psychological Review, 76(1), 31-48.
doi: 10.1037/h0026750 URL |
| [82] |
Tversky, A. (1972). Elimination by aspects: A theory of choice. Psychological Review, 79, 281-299. https://doi.org/10.1037/h0032955
doi: https://doi.org/10.1037/h0032955 URL |
| [83] |
Ulrich, R., & Maienborn, C. (2010). Left-right coding of past and future in language: The mental timeline during sentence processing. Cognition, 117(2), 126-138.
doi: 10.1016/j.cognition.2010.08.001 pmid: 20850112 |
| [84] |
Weger, U. W., & Pratt, J. (2008). Time flies like an arrow: Space-time compatibility effects suggest the use of a mental timeline. Psychonomic Bulletin & Review, 15(2), 426-430.
doi: 10.3758/PBR.15.2.426 URL |
| [85] |
Wiener, J. M., Hölscher, C., Büchner, S., & Konieczny, L. (2012). Gaze behaviour during space perception and spatial decision making. Psychological Research, 76(6), 713-729. https://doi.org/10.1007/s00426-011-0397-5
doi: 10.1007/s00426-011-0397-5 pmid: 22139023 |
| [86] |
Viard, A., Doeller, C. F., Hartley, T., Bird, C. M., & Burgess, N. (2011). Anterior hippocampus and goal-directed spatial decision making. Journal of Neuroscience, 31(12), 4613-4621. https://doi.org/10.1523/JNEUROSCI.4640-10.2011
doi: 10.1523/JNEUROSCI.4640-10.2011 pmid: 21430161 |
| [87] | von Neumann, J., & Morgenstern, O. (1947). Theory of Games and Economic Behavior (2nd ed.). Princeton: Princeton University Press https://archive.org/details/theoryofgamesand030098mbp |
| [88] | von Sobbe, L., Scheifele, E., Maienborn, C., & Ulrich, R. (2019). The space-time congruency effect: A meta-analysis. Cognitive Science, 43(1), e12709. |
| [89] |
Xue, Y., & Brown, D. E. (2003). A decision model for spatial site selection by criminals: A foundation for law enforcement decision support. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 33(1), 78-85. http://dx.doi.org/10.1109/TSMCC.2003.809867
doi: http://dx.doi.org/10.1109/TSMCC.2003.809867 URL |
| [90] | Zhang, Y. Y., Zhou, L., You, X. Q., Li, S., & Liang, Z. Y. (2018). Is intertemporal decision-making based on a temporal discounting process? Evidence from double-dissociation paradigm. Scientia Sinica (Vitae), 48(5), 592-608. |
| [91] |
Zhou, L., Li, A. M., Zhang, L., Li, S., & Liang, Z. Y. (2019). Similarity in processes of risky choice and intertemporal choice: The case of certainty effect and immediacy effect. Acta Psychologica Sinica, 51(3), 337-352. http://dx.doi.org/10.3724/SP.J.1041.2019.00337
doi: http://dx.doi.org/10.3724/SP.J.1041.2019.00337 URL |
| [92] |
Zhou, L., Zhang, Y. Y., Li, S., & Liang, Z, Y. (2018). New paradigms for the old question: Challenge the expectation rule held by risky decision-making theories. Journal of Pacific Rim Psychology, 12(e17), 1-10. http://dx.doi.org/10.1017/prp.2018.4
doi: http://dx.doi.org/10.1017/prp.2018.4 |
| [1] | LIU Hong-Zhi, YANG Xing-Lan, LI Qiu-Yue, WEI Zi-Han. Preference of dimension-based difference in intertemporal choice: Eye-tracking evidence [J]. Acta Psychologica Sinica, 2023, 55(4): 612-625. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||